Matematyka babilońska, podobnie jak inne osiągnięcia cywilizacyjne rozwijane jako spadek po wcześniejszych cywilizacjach Sumerów i Akadów, od dawna zadziwia historyków. Była bardziej rozwinięta od egipskiej; Babilończycy rozwiązywali równania kwadratowe, zestawiali tabliczki mnożenia, znali postępy geometryczne, proporcje i procenty. Wiedza matematyczna pomagała im z pewnością budować precyzyjnie zaprojektowane zigguraty, wielopiętrowe budowle, które były znacznie bardziej skomplikowane architektonicznie niż piramidy. Babilońska gliniana tabliczka datowana na 1770 r. p.n.e. ujawnia stosowanie tego, co dzisiaj nazywamy "twierdzeniem Pitagorasa", tyle tylko, że cały tysiąc lat przed narodzinami greckiego matematyka – wskazał serwis Onet.pl.
Sumerowie, jako pierwsi w historii, stworzyli system zapisu liczbowego oparty na bazie 60. Wybór tej właśnie liczby ma uzasadnienie w jej wielodzielności. Posiadanie przez liczbę 60 12 dzielników zdecydowanie ułatwia zapis ułamków. Babilończycy zmodyfikowali przyjęty od Sumerów i Akadyjczyków system liczbowy, w wyniku czego powstał system pozycyjny. Późniejsze cywilizacje, szczególnie starożytna Grecja, szeroko wykorzystywały osiągnięcia babilońskich matematyków i astronomów dla rozwijania własnych nauk. Niektóre odkrycia, przypisywane Grekom, najwyraźniej były odkryciami Babilończyków – stwierdzono w treści.
Nawiasem mówiąc, europejscy uczeni w średniowieczu wciąż jeszcze korzystali z sześćdziesiętnego systemu liczbowego. To właśnie z Babilonu przyszedł zwyczaj dzielenia godziny na 60 minut, a minuty na 60 sekund. Ale nie tylko – kąt pełny jest podzielony również dzisiaj, podobnie jak w starożytności, na 360 stopni, a nie 100 albo 1000. Trzeba przyznać, że dzięki temu podział godziny albo kąta pełnego na "niewygodne" ułamki, na przykład przez 3, 5, 6 albo 15, jest bardzo praktyczny. Zamiast ułamków dziesiętnych mamy pełne stopnie, minuty i sekundy (również kątowe przy podawaniu współrzędnych geograficznych) – wyjaśniono.
Gliniana tabliczka znaleziona w Iraku, oznaczona przez archeologów numerem IM 67118, nie jest zwyczajnym kawałkiem gliny, jak wiele innych. Jest milczącym świadkiem pomysłowości i wiedzy babilońskich matematyków. Tabliczka datowana na około 1770 r. p.n.e. wskazuje na wykorzystanie twierdzenia Pitagorasa do obliczenia długości przekątnej kwadratu. Jest tylko jeden mały problem: Pitagoras przyszedł na świat ponad 1000 lat później, w 570 r. p.n.e. A to oznacza, że twierdzenie było znane i stosowane znacznie wcześniej – zaznaczono w informacji.
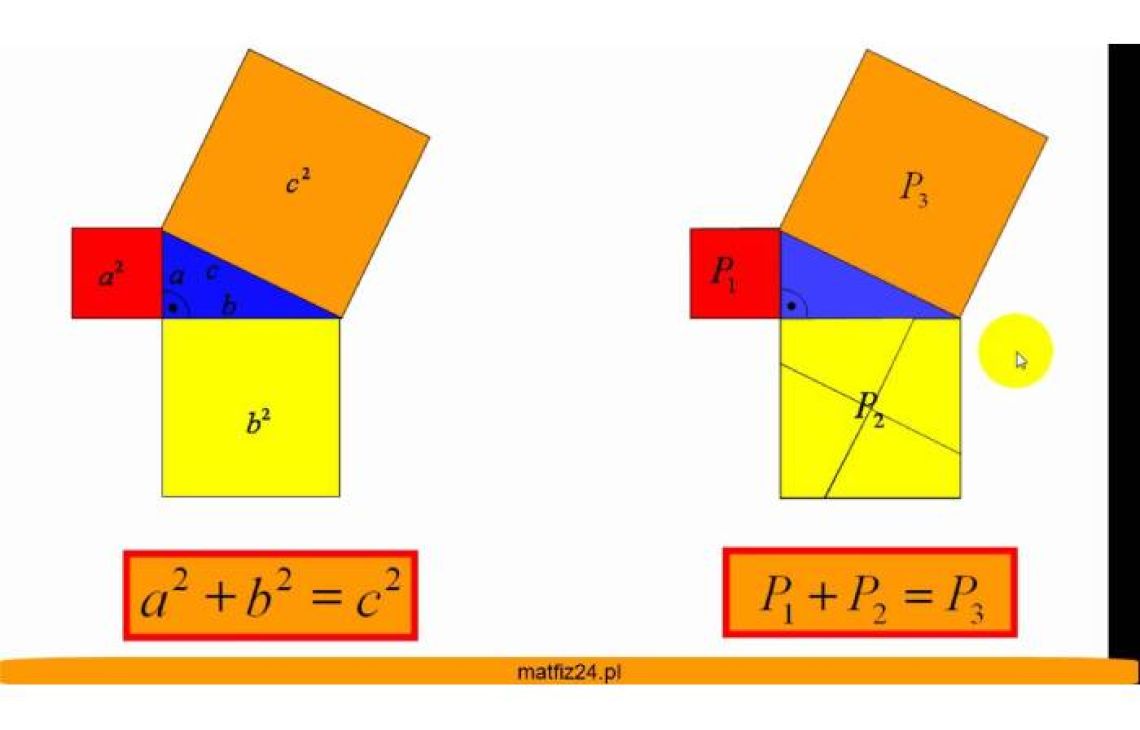
Twierdzenie Pitagorasa ma fundamentalne znaczenie w geometrii. Nazwane tak na cześć starożytnego greckiego filozofa i matematyka określa prostą zależność między bokami trójkąta prostokątnego, a mianowicie: kwadrat przeciwprostokątnej jest równy sumie kwadratów przyprostokątnych. Pomaga określić brakującą długość boku trójkąta prostokątnego, jeśli znane są dwa pozostałe boki. Jego zastosowanie od tysięcy lat ma kluczowe znaczenie w dziedzinach technicznych jak inżynieria i architektura. Na innej tabliczce pochodzącej z lat 1800-1600 p.n.e. również znajduje się kwadrat ze wpisanymi w niego trójkątami – podano dalej.
Każdy, kto uczył się geometrii, pamięta ze szkoły zadania związane z najsłynniejszym chyba w matematyce twierdzeniem. Istnieje podobno ponad 370 dowodów twierdzenia Pitagorasa, w tym dowody młodego Einsteina, Leonarda da Vinci, Euklidesa i wielu innych uczonych. Pitagoras jest nieśmiertelnie związany z odkryciem i udowodnieniem twierdzenia, chociaż istnieją konkretne dowody na to, że twierdzenie Pitagorasa było odkryte i udowodnione przez matematyków babilońskich co najmniej na 1000 lat przed narodzinami sławnego Greka - napisano.
Co ciekawe, twierdzenie znane dzisiaj jako "Pitagorasa" było obecne również w Indiach około VIII w. p.n.e. Występuje w tekście wedyjskim napisanym przez uczonego Baudhāyanę na 300 lat przed narodzinami Pitagorasa. Chociaż Baudhāyana był pierwszym, który o tym równaniu pisał, to wspominali o nim później również inni kapłani wedyjscy - zaznaczono.
Mało tego, twierdzenie Pitagorasa znane było także w Chinach. Według przekazów legendarny władca Huang Di, czyli Żółty Cesarz, panujący około 2600 r. p.n.e., powierzył swemu ministrowi Li Shou sporządzenie zbioru prac o sztuce matematycznej. W tym dziele zostało wyjaśnione, że "w trójkącie prostokątnym suma kwadratów dwóch boków równa się kwadratowi przeciwprostokątnej" – napisano dalej.
Te spostrzeżenia wskazują na możliwy ewolucyjny związek między Indiami, Chinami i Mezopotamią. Co więcej, widać potrzebę poszukiwania wiedzy oraz dzielenia się nią i genialnymi pomysłami podczas podróży po całym świecie. Matematyka jest obecna w życiu człowieka od tysięcy lat, a nasi przodkowie znali ją w stopniu znacznie wyższym, niż nam się czasem wydaje - podkreślono.
Historyczna legenda głosi, że Pitagoras wymyślił swoje twierdzenie, przypatrując się kwadratowym płytkom na podłodze i ścianach pałacu. Znudzony zaczął dzielić kwadraty na trójkąty i tak doszedł do odkrycia związku między długością boków kwadratu i jego przekątnej. Obecnie znawcy tematu przypuszczają, że Pitagoras prawdopodobnie usłyszał o tej zależności boków w trójkącie prostokątnym, kiedy zaczynał interesować się matematyką, a potem spopularyzował to twierdzenie i przyjął za swoje – przypomniano w informacji.
Starożytne biografie Pitagorasa zawierają wiele legend, które po upływie wieków trudno oddzielić od faktów. Z dostępnych źródeł wiadomo jednak, że filozof był bardzo dociekliwy, w młodości dużo się uczył i podróżował. Zdobywał wiedzę od egipskich kapłanów i babilońskich nauczycieli, był uczniem Talesa. Prawdopodobnie w tym czasie zapoznał się z twierdzeniem, które nazwano jego imieniem – czytamy dalej
Nasuwa się pytanie: skoro twierdzenie było już znane, to dlaczego przypisywano je Pitagorasowi? Odpowiedź kryje się w braku pierwotnych źródeł pisanych przez Pitagorasa. Dlatego to, co o nim wiemy, pochodzi wyłącznie z relacji przekazanych głównie przez pitagorejczyków, członków szkoły religijno-filozoficznej założonej przez niego w południowych Włoszech. Aby jak najbardziej uhonorować swojego mistrza, uczniowie Pitagorasa przypisywali mu często nienależne odkrycia, czasem nawet te, których sami dokonali. Fakt, że chcieli oddać cześć swojemu nauczycielowi, niewątpliwie przyczynił się do dalszego utrwalenia i rozgłosu słynnego twierdzenia – stwierdzono w informacji.
Nawet jeśli Pitagoras nie wymyślił słynnego wzoru a² + b² = c², to jego szkoła z pewnością przyczyniła się do jego popularyzacji. W ten sposób, na przestrzeni tysiącleci, ta matematyczna zasada pozostawała związana z imieniem Pitagorasa bez względu na dowody wskazujące na znacznie wcześniejsze pochodzenie. Na szczęście (dla Pitagorasa) nikt dotychczas nie wystąpił z procesem o naruszenie praw autorskich – napisano w podsumowaniu. (jmk)
Foto: YT Marek Duda
Źródło: Onet.pl